§ Обратное вейвлет–преобразование. Основные свойства вейвлета

 

Теоретически доказано, что если сигнал  представлен своим вейвлет–преобразованием , где , то этот сигнал может быть восстановлен по формуле:

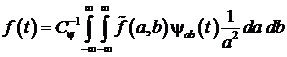,                            (1)

где 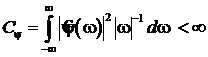 – нормализующий коэффициент, подобный  в преобразовании Фурье;  - спектр Фурье вейвлета

.

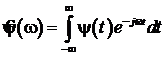Требуемое свойство конечности коэффициента  ограничивает возможный класс функций , которые можно использовать в качестве вейвлетов.

Следует отметить, что прямое вейвлет преобразование

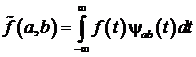                                        (2)

и обратное вейвлет преобразование (1) правомерны, если вейвлеты  образуют ортогональную систему базисных функций

,

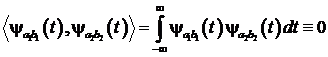для выбранных разных значений .

Определим основные свойства, которыми должен обладать вейвлет:

 

1) Локализация во времени и по частоте, то есть вейвлет определен на конечном временном интервале (например, ) и имеет ограниченный по частоте спектр Фурье

.

2) Нулевое среднее значение

.

Замечание. Считается, что вейвлет обладает лучшими свойствами по выделению небольших кратковременных изменений сигнала, если он имеет несколько нулевых моментов m-го порядка ()

.

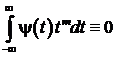3) Ограниченность по энергии

.

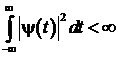4) Автомодельность базиса функций , составленного из вейвлета . Самоподобие (похожесть) функций  одна на другую, так как имеют одинаковое число осцилляций, что и  - базисный вейвлет. Это определяется тем, что функции  получены из  путем масштабирования и сдвига.

 

Помимо рассмотренного вейвлета Хаара  часто используются и иные более гладкие вейвлеты:

a)     Wave-вейвлет , который получается как первая производная от функции Гаусса:

.

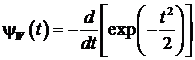Спектр Фурье wave-вейвлета

.

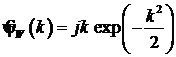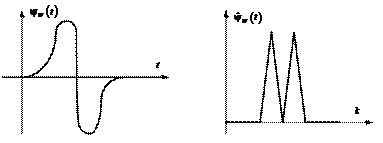
b)    Mhat-вейвлет или «мексиканская шляпа» , получаемый как вторая производная функции Гаусса

.

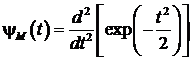Спектр Фурье Mhat-вейвлета

.

     В настоящее время используется несколько десятков различных вейвлетов.

Выбор типа (формы) анализирующего вейвлета, определяется тем, какую информацию необходимо более полно выявить из сигнала.

§ Дискретное вейвлет–преобразование

         По аналогии с преобразованием Фурье, для непрерывного прямого (2) и обратного (1) вейвлет преобразования определяют их дискретные варианты.

         Дискретное прямое вейвлет преобразование определяется формулой:

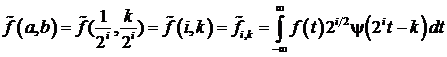.                (3)

В случае перехода к дискретным отсчетам  функции , то в формуле (3) интеграл  заменяется суммой .

Обратное дискретное вейвлет преобразование определяется формулой

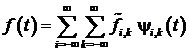,                                      (4)

где  - дискретный вейвлет .

Для дискретных вейвлетов выполняется свойство ортогональности

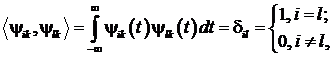
и биортогональности

,

где  - функция Дирака.

Замечание. Прямое и обратное вейвлет преобразование реализованы в модуле Wavelet-анализа пакета Matlab. При этом пользователю представляется широкий набор используемых вейвлетов .

Замечание. Для прямого и обратного вейвлет преобразования разработаны быстрые алгоритмы вычислений, подобные БПФ, что позволяет значительно ускорить расчет вейвлет-спектров.

Замечание. Свойство ортогональности вейвлетов  может не выполняться для выбранной в качестве вейвлета  функции. В этом случае прямое преобразование будет осуществляться с использованием , а обратное с помощью специальных реконструкционных вейвлетов , которые отличаются от  и могут быть найдены по ним.

Такие вейвлеты иногда называют парными (dyadic wavelet) и он имеет следующую реконструкционную формулу (обратного преобразования)

.
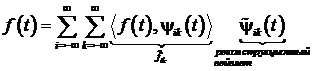